에우클레이데스의 원론
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
에우클레이데스의 《원론》은 고대 그리스 수학자 에우클레이데스가 저술한 13권으로 구성된 수학 저서이다. 기하학, 수론, 무리수 등을 다루며, 공리적 방법과 구성적 방법을 사용하여 수학적 지식을 체계적으로 제시했다. 《원론》은 이전 그리스 수학자들의 저술을 바탕으로 하였으며, 피타고라스 정리, 소수의 무한성 증명 등 중요한 내용을 포함한다. 1482년 첫 인쇄본이 출판된 이후 다양한 언어로 번역되어 널리 읽혔으며, 과학, 철학 등 여러 분야에 영향을 미쳤다. 유클리드의 공리적 접근 방식은 서구 문화에 큰 영향을 미쳤으며, 오늘날에도 수학의 초석으로 여겨진다.
더 읽어볼만한 페이지
| 에우클레이데스의 원론 - [서적]에 관한 문서 | |
|---|---|
| 서지 정보 | |
| 제목 | 원론 |
| 로마자 표기 | Stoikheia |
| 영어 제목 | Elements |
| 저자 | 알렉산드리아의 에우클레이데스 (유클리드) |
| 언어 | 고대 그리스어 |
| 장르 | 수학 |
| 주제 | 평면 및 입체 기하학, 정수론, 비공약수적 선 |
| 출판일 | 기원전 300년경 |
| 내용 | |
| 구성 | 13권 |
| 포함 내용 | 유클리드 기하학의 공리적 전개 정수론의 기초 무리수에 대한 논의 |
| 역사적 중요성 | |
| 영향력 | 20세기 중반까지 모든 수학 교육의 기반 가장 성공적인 수학 교과서 중 하나 |
| 판본 | 1482년 베네치아에서 최초 인쇄 1000개 이상의 판본 존재 (성경 다음으로 많은 판본 추정) |
| 한국어 번역 정보 | |
| 번역자 | 나카무라 코시로 테라사카 히데타카 이토 슌타로 이케다 미에 사이토 켄 미우라 노부오 |
| 출판사 | 쿄리츠 출판 도쿄 대학 출판회 |
| 출판일 | 2011년 5월 25일 (쿄리츠 출판) 2008년 1월 28일 (도쿄 대학 출판회) |
| ISBN | ISBN 978-4-320-01965-2 (쿄리츠 출판) ISBN 978-4-13-065301-5 (도쿄 대학 출판회) ISBN 978-4-13-065302-2 (도쿄 대학 출판회) |
| 기타 | |
| 관련 항목 | 기하학 원본 |
| 분류 | 수학 |
 | |
 | |
2. 역사


4세기경 알렉산드리아의 테온은 유클리드의 판본을 만들었는데, 이는 매우 널리 사용되었다. 1808년 프랑수아 페이라드가 바티칸 도서관에서 테온의 판본에서 파생되지 않은 필사본을 발견하기 전까지 테온의 판본은 유일하게 남아있는 자료였다.[3] 이 필사본은 요한 루드비히 하이베르크 필사본으로, 900년경 비잔틴 공방에서 제작되었으며 현대 판본의 기초가 되었다.[3]
아랍어 번역은 약 760년경 비잔틴 제국으로부터 《원론》을 받은 아랍인들에 의해 이루어졌다. 이 버전은 하룬 알 라시드(800년경) 치하에서 번역되었다.[3] 비잔틴 학자 카이사레아의 아레타스는 9세기 말 유클리드의 현존하는 그리스어 필사본 중 하나를 베끼도록 의뢰했다.[3] 비잔틴 제국에는 알려져 있었지만, 《원론》은 약 1120년까지 서유럽에서 사라졌는데, 이때 영국 수도사 배스의 아델라드가 아랍어 번역본을 라틴어로 번역했다.[3]
최초의 인쇄본은 1482년에 출판되었고(캄파누스의 번역을 기반으로 함),[1] 그 이후 여러 언어로 번역되어 약 천 개의 다른 판본으로 출판되었다. 테온의 그리스어 판본은 복원되어 1533년에 출판되었으며,[8] 1570년에 존 디는 헨리 빌링슬리가 낸 최초의 영어판에 "수학적 서문"과 함께 많은 주석과 보충 자료를 제공했다.
그리스어 텍스트의 사본이 여전히 존재하며, 일부는 바티칸 도서관과 옥스퍼드의 보들리안 도서관에서 찾을 수 있다.
2. 1. 이전 연구 기반
학자들은 《원론》이 이전 그리스 수학자들의 저서를 바탕으로 한 명제들의 집대성이라고 믿고 있다.[1]프로클로스 (412–485 AD)는 에우클레이데스보다 약 7세기 후에 살았던 그리스 수학자인데, 《원론》에 대한 그의 주석에서 다음과 같이 썼다. "에우클레이데스는 《원론》을 집필하면서 크니도스의 에우독소스의 많은 정리를 수집하고, 테아이테토스의 많은 것을 완벽하게 하였으며, 선배들이 다소 애매하게 증명했던 것들을 반박할 수 없는 증명으로 이끌었다."
피타고라스 ( 기원전 570–495년)는 아마도 1권과 2권 대부분의 자료를 제공했으며, 키오스의 히포크라테스 ( 기원전 470–410년, 더 잘 알려진 코스의 히포크라테스와는 다름)는 3권의 자료를 제공했으며, 크니도스의 에우독소스 ( 기원전 408–355년)는 5권의 자료를 제공했으며, 4, 6, 11, 12권은 아마도 다른 피타고라스 학파나 아테네의 수학자들에게서 나왔을 것이다.[2] 《원론》은 또한 키오스의 히포크라테스가 저술한 이전의 교과서를 기반으로 했을 수 있으며, 그는 또한 도형을 지칭하기 위해 문자를 사용하는 방식을 처음 사용했을 수 있다.[3] 비슷한 다른 작품들은 마그네시아의 테우디우스, 레온, 그리고 콜로폰의 헤르모티무스에 의해 쓰여졌다고 알려져 있다.[4][5]
2. 2. 텍스트 전승
옥시린쿠스 파피루스에서 발견된 유클리드 ''원론''의 조각은 매우 오래된 필사본의 일부이다.[3] 4세기경 알렉산드리아의 테온은 유클리드의 판본을 만들었는데, 이 판본은 널리 사용되었다. 1808년 프랑수아 페이라드가 바티칸 도서관에서 테온의 판본에서 파생되지 않은 필사본을 발견하기 전까지 테온의 판본은 유일하게 남아있는 자료였다. 이 필사본은 요한 루드비히 하이베르크 필사본으로 불리며, 900년경 비잔틴 공방에서 제작되었으며 현대 판본의 기초가 되었다.[3]아랍인들은 약 760년경 비잔틴인으로부터 《원론》을 받았다. 이 버전은 하룬 알 라시드(800) 치하에서 아랍어로 번역되었다.[3] 카이사레아의 아레타스는 9세기 말 유클리드의 현존하는 그리스어 필사본 중 하나를 베끼도록 의뢰했다.[3] 비잔틴 제국에는 알려져 있었지만, 《원론》은 약 1120년까지 서유럽에서 사라졌는데, 이때 영국 수도사 배스의 아델라드가 아랍어 번역본을 라틴어로 번역했다.[3] 아델라드의 번역은 12세기에 아랍어로 번역된 ''원론''을 라틴어로 번역한 가장 오래된 번역본이다.[3]
12세기에는 시칠리아의 팔레르모에서 그리스어-라틴어 번역본이 만들어졌다. 번역자는 프톨레마이오스의 알마게스트를 라틴어로 번역하기 위해 팔레르모를 방문한 살레르노 출신의 익명의 의학 학생으로 알려져 있다. 유클리드 필사본은 현존하며 상당히 완전하다.[4]
배스의 아델라드(아델라드 I세)의 번역 이후, 아랍어에서 많은 번역이 이루어졌다. 이 시기의 주목할 만한 번역가로는 1140년경 판본을 쓴 카린티아의 헤르만, 1251년 이전 또는 그 시기에 쓰여진 로버트 오브 체스터(그의 필사본은 총칭하여 아델라드 II세), 요하네스 데 티네무에[5], 아마도 타인머스의 존으로도 알려짐(그의 필사본은 총칭하여 아델라드 III세), 12세기 말, 그리고 크레모나의 제라르 (1120년 이후 1187년 이전)가 있다.[6][7] 노바라의 캄파누스는 이러한 아랍어 번역에 크게 의존하여 1260년 이전에 자신의 판본을 만들었다. 16세기에 그리스어 필사본을 사용할 수 있게 되기 전까지 라틴어 판본을 지배하게 된 것은 캄파누스의 판본이었다. 1482년 이전에 제작된 100개 이상의 캄파누스 필사본이 오늘날에도 남아 있다.[6][7]
첫 번째 인쇄본은 1482년에 출판되었고(캄파누스의 번역을 기반으로 함),[6] 그 이후 여러 언어로 번역되어 약 천 개의 다른 판본으로 출판되었다. 테온의 그리스어 판본은 복원되어 1533년에 출판되었으며,[8] 파리 gr. 2343과 Venetus Marcianus 301을 기반으로 했다.[9] 1570년에 존 디는 헨리 빌링슬리가 낸 최초의 영어판에 "수학적 서문"과 함께 많은 주석과 보충 자료를 제공했다.
그리스어 텍스트의 사본이 여전히 존재하며, 일부는 바티칸 도서관과 옥스퍼드의 보들리안 도서관에서 찾을 수 있다. 현존하는 필사본은 품질이 다양하며, 항상 불완전하다.
3. 구성 및 내용
《원론》은 총 13권으로 구성되어 있으며, 크게 기하학, 비례론, 수론, 무리수에 대한 내용을 다룬다. 각 권의 주요 내용은 다음과 같다.
| 권 | I | II | III | IV | V | VI | VII | VIII | IX | X | XI | XII | XIII | 합계 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 정의 | 23 | 2 | 11 | 7 | 18 | 4 | 22 | – | – | 16 | 28 | – | – | 131 |
| 공준 | 5 | – | – | – | – | – | – | – | – | – | – | – | – | 5 |
| 공통 관념 | 5 | – | – | – | – | – | – | – | – | – | – | – | – | 5 |
| 명제 | 48 | 14 | 37 | 16 | 25 | 33 | 39 | 27 | 36 | 115 | 39 | 18 | 18 | 465 |
- 제1권 ~ 제4권: 평면 기하학을 다룬다. 피타고라스 정리[23], 기하학적 대수, 탈레스의 정리 등이 여기에 해당한다.
- 제5권: 에우독소스의 비율 이론을 다룬다.[23]
- 제6권: 비율 이론을 닮음 도형에 적용한다.[23]
- 제7권 ~ 제9권: 수론을 다룬다. 유클리드 호제법, 산술의 기본 정리, 소수의 무한성, 완전수 등이 여기에 해당한다.[23]
- 제10권: 무리수를 다룬다.[21]
- 제11권 ~ 제13권: 입체 기하학을 다룬다. 평행육면체, 정육면체, 각기둥, 원뿔, 피라미드, 원기둥, 구, 정다면체 등이 여기에 해당한다.[23]
비유클리드 기하학의 등장으로 인해, 평행선 공준을 바탕으로 하는 기하학은 유클리드 기하학으로 불리게 되었다.
제14권, 제15권도 존재하지만, 이는 후대에 추가된 것으로 알려져 있다.[22]
제1권부터 제4권까지, 그리고 제6권은 평면의 초등 기하에 대한 내용으로, 피타고라스 학파 등에 의해 이미 체계화된 정보를 유클리드가 재편집했을 가능성이 높다. 제5권과 제12권은 플라톤 학파 수학자 에우독소스의 업적이며, 제10권과 제13권은 테아이테토스의 업적으로 알려져 있다. 따라서 유클리드는 기존의 지식과 최신 학술 성과를 종합하여 『원론』을 편찬한 것으로 보인다.
3. 1. 제1권 ~ 제4권: 평면 기하학
에우클레이데스의 원론 제1권부터 제4권까지는 2차원(평면) 기하학에 관한 내용을 담고 있다.[23]- 제1권: 필수적이고 예비적인 정의와 설명, 공준과 공리로 시작한다. 제1권의 정리 중에는 합동, 평행선, 직선으로 이루어진 도형 등에 관한 친숙한 정리들이 포함되어 있다. 마지막 두 정리인 정리 47과 48은 피타고라스 정리와 그 역이다. 18세기까지 기하학 교과서로 쓰인 이유도 여기에 있다.
- 제2권: 겨우 14개의 정리만을 포함하고 있는 작은 책으로, 주로 피타고라스 학파의 기하 대수학을 다룬다. 이 책의 정리 12와 13은 근본적으로 오늘날 코사인 법칙으로 알려진 피타고라스 정리의 일반화이다.
- 제3권: 39개의 정리로 이루어졌으며, 원, 현, 할선, 접선, 연관된 각도의 측정 등에 관한 정리들을 포함하고 있다.
- 제4권: 16개의 정리로 이루어져 있으며, 자와 컴퍼스를 이용한 작도, 주어진 원에 내접하는 경우와 외접하는 경우의 작도, 정다각형의 작도를 포함하고 있다.
| 권수 | 정의 | 공준 | 공리 | 명제 | 내용 |
|---|---|---|---|---|---|
| 제1권 | 23 | 5 | 5 (또는 9) | 48 | 평면 도형의 성질 |
| 제2권 | 2 | 0 | 0 | 14 | 면적의 변형 (소위 기하학적 대수) |
| 제3권 | 11 | 0 | 0 | 37 | 원의 성질 |
| 제4권 | 7 | 0 | 0 | 16 | 원에 내접·외접하는 다각형 |
평면의 초등 기하에 대해 서술되어 있는 것은 제1권, 제2권, 제3권, 제4권과 제6권이다. 다만, 이 내용은 유클리드 본인의 업적이라기보다는, 그 이전에 피타고라스 학파 등의 공헌에 의해 유클리드 시대 이전부터 이미 체계화되어 있던 정보를 재편찬한 것일 가능성이 높다.
『원론』에서는 몇 가지 정의에서 시작하여, 5개의 공준(요청)과 5개(또는 9개)의 공리(공통 개념)가 제시되어 있다. 논의의 전제가 되는 점, 선, 직선, 면, 각, 원, 중심 등의 개념이 정의되고, 다음과 같은 5개의 공준을 참으로 받아들임으로써 작도의 문제의 기초를 명확히 하고 있다.
# 임의의 한 점에서 다른 한 점으로 직선을 긋는 것
# 유한한 직선을 연속적으로 똑바로 연장하는 것
# 임의의 중심과 반지름으로 원을 그리는 것
# 모든 직각은 서로 같다
# 직선이 2개의 직선과 교차할 때, 같은 쪽의 내각의 합이 2직각보다 작은 경우, 그 2개의 직선이 한없이 연장될 때, 내각의 합이 2직각보다 작은 쪽에서 교차한다.
이 중에서 5번째 공준에 대해서는 고대부터 다른 공리, 공준에 비해 두드러지게 복잡하다는 점에서 자명하다고 하기에는 의문이 제기되었고, 이 의문으로 인해 근대에 이르러 이 공준이 성립하지 않는 기하학인 비유클리드 기하학의 발단이 되었다.
더욱이 공준 뒤에 다음과 같은 공리가 제시된다. 이것은 모든 학문에 공통된 진리로서 받아들여지며, 연구에 있어서 항상 참조해야 할 것으로 여겨진다.
# 같은 것에 같은 것은 서로 같다.
# 같은 것에 같은 것을 더한 경우, 그 합은 같다.
# 같은 것에서 같은 것을 뺀 경우, 나머지는 같다.
# [부등한 것에 같은 것을 더한 경우, 그 합은 부등하다.]
# [같은 것의 2배는 서로 같다.]
# [같은 것의 반은 서로 같다.]
# 서로 겹쳐지는 것은 서로 같다.
# 전체는 부분보다 크다.
# [2선분은 면적을 둘러싸지 않는다.]
단, []로 둘러싸인 공리는 공리에 포함하지 않는 경우가 있다. 제5공리는 제2공리에서 유도된다. 또한 제9공리를 현대적으로 바꿔 말하면 "서로 다른 2점을 지나는 직선은 단 1개만 존재한다"가 된다. 제9공리는 기하학에 관한 것이므로, 원래는 공준에 포함될 수 있는 것으로 생각된다.
3. 2. 제5권: 비율 이론
Τὰ στοιχεῖα|타 스토이케이아grc의 제5권은 에우독소스의 비율 이론을 다루고 있으며, 수학적인 문헌 중에서도 뛰어난 걸작으로 평가받는다.[23] 제5권은 총 25개의 명제와 18개의 정의로 구성되어 있다.[21]3. 3. 제6권: 도형에의 응용
에우독소스의 비율 이론을 닮음 도형 연구에 응용하고 있다.[23] 제6권에는 4개의 정의와 33개의 명제가 있다.[21]3. 4. 제7권 ~ 제9권: 수론
제7권은 두 개 이상의 정수에 대한 최대공약수를 구하는 방법(유클리드 호제법)으로 시작된다.[23] 또한 초기 피타고라스 학파의 비율 이론에 대한 설명을 발견할 수 있다.[23]제8권은 주로 연비례와 그것과 관련된 등비수열을 다루고 있다. 만약 a : b = c : d가 성립하면 a, b, c, d는 등비수열을 형성한다.[23]
제9권에는 수론에서 중요한 많은 정리들이 있는데, 먼저 정리 14는 ‘산술의 기본 정리(Fundamental theorem of arithmetic)’ 즉, “1보다 큰 임의의 정수는 반드시 소수들의 곱으로 표현될 수 있으며 근본적으로 단 한 가지 방법으로 표현된다.”는 정리와 동치이다.[23] 정리 20에서 ‘소수의 개수는 무한하다.’는 사실에 대한 매우 세련된 증명을 찾아볼 수 있다.[23] 정리 35는 등비수열의 첫 n개의 항의 합에 대한 공식을 기하적으로 유도했다.[23] 그리고 이 책의 마지막 정리인 정리 36은 짝수인 완전수를 만드는 놀라운 공식을 증명하고 있다.[23]
제7권부터 제9권까지는 수론에 대한 내용을 담고 있으며, 각 권의 내용은 다음과 같다.[21]
| 권수 | 정의 | 명제 | 내용 |
|---|---|---|---|
| 제7권 | 22 | 39 | 수론 |
| 제8권 | 0 | 27 | 수론 |
| 제9권 | 0 | 36 | 수론 |
3. 5. 제10권: 무리수
제10권은 무리수를 다루며, 비가측 선분의 제곱근을 분류한다.[21] 총 115개의 명제를 포함하며, 정의는 세 부분으로 나뉜다. 제1군은 4개, 제2군은 6개, 제3군은 6개의 정의를 포함한다.[21]3. 6. 제11권 ~ 제13권: 입체 기하학
제11권에서는 3차원 기하학의 기본 개념을 다룬다. 선과 면, 면과 면, 평행육면체, 정육면체, 각기둥 등이 여기에 해당한다.[23] 정의는 29개가 있다.[21]제12권에서는 원의 면적과 각뿔, 각기둥, 원뿔, 원기둥, 구의 체적을 다룬다. 단, 원주율은 사용하지 않고, 원의 면적은 지름의 제곱에 비례하고 구의 체적은 지름의 세제곱에 비례함을 이용한다.[23] 명제는 18개이다.[21]
제13권에서는 정다면체에 대해 다루는데, 정사면체, 정육면체, 정팔면체, 정십이면체, 정이십면체의 다섯 종류만이 정다면체임을 증명한다.[23] 명제는 18개이다.[21]
4. 유클리드의 방법론과 표현 방식
유클리드의 공리적 접근 방식과 구성적 방법은 널리 영향을 미쳤다.[1]
유클리드의 많은 명제는 컴퍼스와 자를 사용하여 객체를 구성하는 단계를 상세히 설명함으로써 어떤 도형의 존재를 증명하는 구성적 명제였다. 그의 구성적 접근 방식은 직선과 원의 존재를 명시하는 첫 번째와 세 번째 공준에서도 나타난다. 그는 이전 정의에 따라 선과 원이 존재한다고 진술하는 대신, 선과 원을 '작도'하는 것이 가능하다고 진술한다. 또한, 증명 중 하나에서 도형을 사용하려면, 이전 명제에서 그것을 구성해야 했다. 예를 들어, 피타고라스 정리를 증명하기 위해 직각 삼각형의 변에 먼저 정사각형을 내접했지만, 한 명제 이전에 주어진 선에 정사각형을 구성한 후에야 가능했다.[2]

고대 수학 텍스트에서 흔히 볼 수 있듯이, 명제가 여러 경우에 증명이 필요한 경우, 유클리드는 종종 그 중 하나(주로 가장 어려운 경우)만 증명하고 나머지는 독자에게 맡겼다. 테온과 같은 후대의 편집자들은 종종 이러한 경우에 대한 자체 증명을 삽입했다.
유클리드의 제시 방식은 그의 시대에 통용되던 수학적 아이디어와 표기법에 의해 제한되었으며, 현대 독자에게는 어떤 부분에서 어색하게 느껴진다. 예를 들어, 2직각보다 큰 각에 대한 개념이 없었고, 숫자 1은 때때로 다른 양의 정수와 별도로 취급되었으며, 곱셈이 기하학적으로 처리되었기 때문에 3개 이상의 서로 다른 숫자의 곱을 사용하지 않았다. 수론에 대한 기하학적 처리는 대안이 매우 어색한 알렉산드리아 숫자 체계였기 때문일 수 있다.
각 결과의 제시는 양식화된 형태로 제공되며, 이는 유클리드가 발명한 것은 아니지만, 전형적인 고전적인 것으로 인식된다. 유클리드의 제시 방식은 여섯 가지 다른 부분으로 구성되어 있다.
| 순서 | 내용 |
|---|---|
| 첫째 | 일반적인 용어로 결과를 진술하는 명제(명제의 진술) |
| 둘째 | 설정. 도형을 제공하고 특정 기하학적 객체를 문자로 나타낸다. |
| 셋째 | 정의 또는 명세. 특정 도형의 관점에서 명제를 다시 진술한다. |
| 넷째 | 작도 또는 기계. 원래 도형은 증명을 위해 확장된다. |
| 다섯째 | '증명' |
| 여섯째 | 결론. 증명에서 도출된 특정 결론을 명제의 일반적인 용어로 진술함으로써 증명을 명제와 연결한다. |
결과로 이어진 추론 방식에 대한 표시는 제공되지 않지만, ''자료''는 ''원론''의 처음 네 권에서 만나는 유형의 문제에 접근하는 방법에 대한 지침을 제공한다. 일부 학자들은 유클리드가 증명에서 도형을 사용하는 것에 대해 결점을 찾으려고 시도했으며, 특히 제1권의 명제 II와 관련하여 일반적인 기본 논리보다는 그려진 특정 도형에 의존하는 증명을 썼다고 비난했다. 그러나 이 명제에 대한 유클리드의 원래 증명은 일반적이고 유효하며, 주어진 구성의 예를 설명하는 데 사용된 도형에 의존하지 않는다.
5. 비판
에우클레이데스의 《원론》에는 몇 가지 오류가 있다. 몇몇 기본적인 정리는 에우클레이데스가 명시적으로 언급하지 않은 공리를 사용하여 증명되었다. 몇몇 증명은 직관적이지만 명시적으로 증명되지 않은 가정을 사용하여 오류를 범하고 있다. 수학자이자 역사가인 W. W. 로스 볼은 이러한 비판에 대해 "2천년 동안 《원론》이 해당 분야의 일반적인 교과서였다는 사실은 그 목적에 부적합하지 않다는 강력한 추정을 제기한다."라고 언급했다.[16]
후대의 편집자들은 에우클레이데스의 암묵적인 공리적 가정을 공식적인 공리 목록에 추가했다.[16] 예를 들어, 제1권의 첫 번째 작도에서 에우클레이데스는 반지름 거리에 중심이 있는 두 원이 두 점에서 교차한다는 전제를 사용했는데, 이는 가정되거나 증명되지 않은 것이다.[16]
에우클레이데스의 오류는 최소한 1882년까지 거슬러 올라가는데, 이때 파슈가 누락된 공리를 발표했다. 모든 오류를 찾으려는 초기 시도에는 힐베르트의 기하학 공리와 타르스키의 공리가 포함된다. 2018년, 마이클 비슨 등은 컴퓨터 증명 보조자를 사용하여 에우클레이데스의 공리와 유사한 새로운 공리 집합을 만들고 해당 공리에 유효한 증명을 생성했다.[16]
비슨 등은 제1권만 검토했으며, 누락된 공리, 불필요한 공리, 논리적 틈새(예: 점이 공선임을 증명하지 못하는 경우), 누락된 정리(예: 각도는 자기 자신보다 작을 수 없음) 및 명백한 잘못된 증명과 같은 오류를 발견했다. 잘못된 증명은 제1권, 증명 7 및 제1권, 명제 9에 있었다.
6. 영향
''원론''은 논리를 수학에 적용한 걸작으로 여겨지며, 역사적으로 여러 과학 분야에 큰 영향을 미쳤다. 니콜라우스 코페르니쿠스, 요하네스 케플러, 갈릴레오 갈릴레이, 아이작 뉴턴, 알베르트 아인슈타인과 같은 과학자들은 ''원론''의 영향을 받아 자신의 연구에 적용했다.[10][11] 토머스 홉스, 바뤼흐 스피노자, 앨프리드 노스 화이트헤드, 버트런드 러셀과 같은 수학자 및 철학자들은 유클리드의 공리화된 연역적 구조를 채택하여 각자의 분야에 맞는 독자적인 "원론"을 만들려고 시도했다.
유클리드 기하학의 엄격한 아름다움은 서구 문화에서 완벽함과 확실성의 초월적인 세계를 엿볼 수 있는 것으로 여겨졌다. 에이브러햄 링컨은 유클리드의 책을 안장에 넣어 가지고 다니며 밤늦도록 등불 아래에서 공부했다고 알려져 있다.[12] 에드나 세인트 빈센트 밀레이는 소네트 "유클리드만이 벌거벗은 아름다움을 보았다"에서 유클리드를 찬양했다. 알베르트 아인슈타인은 어릴 적 자신에게 큰 영향을 미친 두 가지 선물로 ''원론''과 자석 나침반을 기억하며, 유클리드를 "거룩한 작은 기하학 책"이라고 언급했다.[13][14]
''원론''은 대부분의 수학적 지식을 논리적으로 제시했기 때문에 성공할 수 있었다. 유클리드는 소수의 공리에서 심오한 결과에 이르기까지 그의 주제를 체계적으로 전개했고, ''원론'' 전체에 걸쳐 그의 접근 방식이 일관성을 유지했기 때문에 약 2,000년 동안 교과서로 사용될 수 있었다. ''원론''은 오늘날에도 현대 기하학 책에 영향을 미치고 있으며, 그의 논리적이고 공리적인 접근 방식과 엄격한 증명은 수학의 초석으로 남아 있다.
유클리드가 현대 수학에 미친 가장 주목할 만한 영향 중 하나는 평행선 공준에 대한 논의이다. 유클리드는 《원론》 제1권에서 다섯 개의 공준을 제시하는데, 그중 다섯 번째 공준은 다음과 같다.
> 어떤 선분이 두 개의 직선 선과 만나서 같은 쪽에 있는 두 개의 내각의 합이 두 개의 직각보다 작을 경우, 두 직선은 무한히 연장될 때 그 각의 합이 두 직각보다 작은 쪽에서 만난다.
이 공준은 다른 네 개의 공준에 비해 복잡해 보여서 수 세기 동안 수학자들을 괴롭혔다. 많은 시도가 나머지 네 개의 공준을 기반으로 다섯 번째 공준을 증명하려 했지만, 성공하지 못했다. 결국 1829년, 수학자 니콜라이 로바체프스키는 예각 기하학(또는 쌍곡 기하학)에 대한 설명을 발표했는데, 이는 평행선 공준의 다른 형태를 가정하는 기하학이다. 다섯 번째 공준 없이, 또는 다섯 번째 공준의 다른 버전(타원 기하학)을 사용하여 유효한 기하학을 만들 수 있다. 다섯 번째 공준을 주어진 것으로 받아들이면 유클리드 기하학이 된다.
7. 판본 및 번역
알렉산드리아의 테온은 4세기경 유클리드의 판본을 만들었는데, 이는 매우 널리 사용되어 프랑수아 페이라드가 1808년 바티칸 도서관에서 테온의 판본에서 파생되지 않은 필사본을 발견하기 전까지 유일하게 남아 있는 자료였다.[3] 이 필사본은 요한 루드비히 하이베르크 필사본으로, 900년경 비잔틴 공방에서 제작되었으며 현대 판본의 기초가 되었다.[3]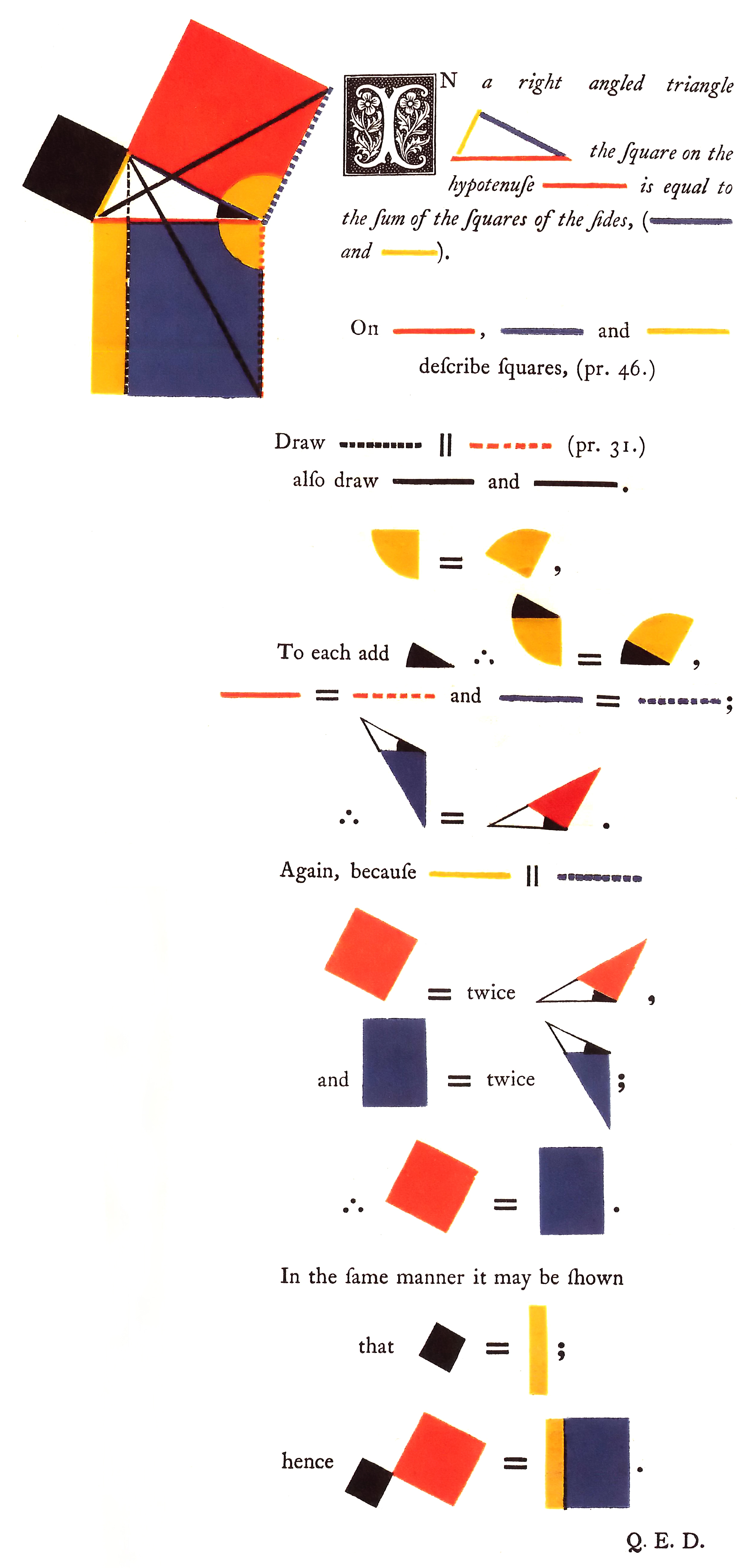
- 4세기, 알렉산드리아의 테온, 서기 888년 필사본 현존.
- 9세기, 테온 이전 페이라르 바티칸 그리스어 190
- 1482년 이전, 많은 중세 판본
- 1460년대, 레기오몬타누스(미완성)
- 1482년, 에르하르트 라트돌트(베네치아), ''초판본''(라틴어)[17][18]
- 1533년, 시몬 그리나에우스의 그리스어 텍스트 ''초판본''[19]
- 1557년, 장 마니앵과 피에르 드 몽도레 출판, 스테파누스 그라실리스 검토 (명제만 있고, 전체 증명은 없음, 원본 그리스어와 라틴어 번역 포함)
- 1572년, 코만디누스 라틴어 판
- 1574년, 크리스토프 클라비우스
- 1883–1888년, 요한 루트비히 하이베르크
| 언어 | 번역자 | 연도 |
|---|---|---|
| 영어 | 헨리 빌링슬리 | 1570년 |
| 영어 | 아이작 배로 | 1660년 |
| 영어 | 찰스 스카버러 | 1705년 |
| 영어 | 로버트 심슨 | 1756년 |
| 영어 | 토마스 리틀 히스 | 1908년 (1926년 개정) |
| 라틴어 | 1505년 | |
| 이탈리아어 | 니콜로 타르탈리아 | 1543년 |
| 독일어 | 요한 셰우벨 | 1558년 |
| 프랑스어 | 피에르 드 몽도레, 베지에르 | 1564–1566년 |
| 이탈리아어 | 코만디누스 | 1575년 |
| 아랍어 | 메디치 인쇄소 (나시르 알딘 알투시의 아랍어 번역판 편집본, 유클리드 기하학 원론) | 1594년 |
| 중국어 | 마테오 리치, 쉬광치 | 1607년 |
| 네덜란드어 | 프란스 반 스코텐 | 1617년 |
| 프랑스어 | 피에르 에리곤 | 1639년 |
| 산스크리트어 | 자간나타 삼라트 (나시르 알딘 알투시의 아랍어 번역 기반) | 1720년대 |
| 히브리어 | 바루크 쉬크 오브 시클로브 | 1780년 |
| 프랑스어 | 프랑수아 페이라르 | 1804년 |
| 러시아어 | 바첸코-자하르첸코 | 1880년 |
| 체코어 | 프란티세크 세르비트 | 1907년 |
| 한국어 | 사이토 켄, 미우라 노부오 외 | 2008년 (1권), 2015년 (2권), 2010년 (4권) |
참조
[1]
논문
Digging for Structure into the Elements: Euclid, Hilbert, and Mueller
https://core.ac.uk/d[...]
Historia Mathematica
1985
[2]
논문
Plato as "Architect of Science"
https://philarchive.[...]
Phonesis
1998
[3]
웹사이트
The Earliest Surviving Manuscript Closest to Euclid's Original Text (Circa 850)
http://historyofinfo[...]
[4]
학술지
Euclides Graeco-Latinus: A Hitherto Unknown Medieval Latin Translation of the Elements Made Directly from the Greek
1967
[5]
학술지
John of Tynemouth alias John of London: Emerging Portrait of a Singular Medieval Mathematician
https://www.jstor.or[...]
1990
[6]
서적
Euclid in Medieval Europe
https://math.berkele[...]
Benjamin catalogue
1989
[7]
웹사이트
DigiVatLib
https://digi.vatlib.[...]
2023-11-20
[8]
웹사이트
Mathematical Treasures - Greek Edition of Euclid's Elements {{!}} Mathematical Association of America
https://maa.org/pres[...]
[9]
서적
The thirteen books of Euclid's Elements. Vol. 1: Introduction and books I, II
Dover Publications
1956
[10]
뉴스
One of the world's most influential math texts is getting a beautiful, minimalist edition
https://www.theverge[...]
2017-09-02
[11]
뉴스
How Euclid once ruled the world
https://plus.maths.o[...]
[12]
웹사이트
Euclid as Founding Father
https://nautil.us/is[...]
[13]
웹사이트
Einstein as a Student
http://www.chem.harv[...]
Department of Chemistry and Chemical Biology, Harvard University, Cambridge, MA
[14]
웹사이트
Albert Einstein – Young Einstein
http://www.albertein[...]
2018-04-29
[15]
간행물
Euclid's Elements
Clark University
1997-06
[16]
학술지
Proof-checking Euclid
https://www.michaelb[...]
2024-09-25
[17]
문서
Alexanderson Greenwalt
2012
[18]
웹사이트
Editio Princeps of Euclid's Elements, the Most Famous Textbook Ever Published : History of Information
https://www.historyo[...]
2023-07-28
[19]
웹사이트
The First Printed Edition of the Greek Text of Euclid is also the First Edition to Include the Diagrams within the Text : History of Information
https://historyofinf[...]
2023-07-28
[20]
웹사이트
JNUL Digitized Book Repository
http://aleph500.huji[...]
2018-04-29
[21]
문서
p. 489.より引用。
[22]
문서
Heiberg&Menge(1883-1916)
[23]
문서
오늘날의 수학자들은 ‘공리’와 ‘공준’이라는 단어를 형식논리학의 토대에서 사실상 동의어로 사용하지만, 고대 그리스의 에우클레이데스는 그 두 단어를 채택하는 데 공리는 모든 학문 분야에 공통인 초기 가정인 반면에 공준은 특수한 분야에 한정되는 것이라는 점에서 차이를 두었다고 여겨진다.
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com

